Getting Started with Machine Learning

The classic definition of Machine Learning is: Machine learning is a field of computer science that gives computers the ability to learn without being explicitly programmed.

Machine learning is a core sub-area of artificial intelligence; it enables computers to get into a mode of self-learning without being explicitly programmed. When exposed to new data, these computer programs are enabled to learn, grow, change, and develop by themselves.While the concept of machine learning has been around for a long time, (an early and notable example: Alan Turing’s famous WWII Enigma Machine) the ability to apply complex mathematical calculations to big data automatically iteratively and quickly has been gaining momentum over the last several years.

To better understand the uses of machine learning, consider some of the instances where machine learning is applied: the self-driving Google car, cyber fraud detection, online recommendation engines like friend suggestions on Facebook, Netflix showcasing the movies and shows you might like, and “more items to consider” and “get yourself a little something” on Amazon are all examples of applied machine learning.

Now there are different categories of Machine Learning, each having its own importance. The categories of Machine Learning algorithms are:

• Supervised Machine Learning
• Unsupervised Machine Learning
• Semi Supervised Machine Learning
• Reinforcement Learning

A very detailed and comprehensive explanation of all these categories is provided in this link

Let’s start with Supervised Learning in this blog.

Supervised Learning.

This kind of learning is possible when inputs and the outputs are clearly identified, and algorithms are trained using labeled examples. Supervised Learning is broadly divided into 2 parts:

• Regression: If the desired output consists of prediction of one or more continuous variables, then the task is called regression. An example of a regression problem would be the prediction of the length of a salmon as a function of its age and weight.

• Linear Regression
• Polynomial Regression
• Stepwise Regression
• Ridge Regression
• Lasso Regression
• Classification: Classification is a learning approach in which the computer program learns from the data input given to it and then uses this learning to classify new observation.
  • Logistic Regression
  • Decision Trees
  • Naive Bayes
  • K-Nearest Neighbours
  • Neural Networks

Before we start, we need to clear some ML notations.

Attributes or Features: An attribute is a property of an instance that may be used to determine its classification. In the IRIS dataset, the attributes are the petal and sepal length and width. They are also known as Features.

Target variable: In the machine learning context, target variable is the variable that is or should be the output. In the IRIS dataset target variables are the 3 flower species.

Now machine learning algorithms can be applied in 2 ways:

1) Implement your own algorithm from scratch.

2) Use Third party libraries like Google’s Scikit Learn.

It is highly recommended that you code your algorithms from scratch while learning to have a thorough understanding but as per industry standards, you are not generally expected to implement individual algorithms. Most of them use scikit or some other library for all the work. This blog will contain code for both types i.e from scratch and sklearn code.

Now lets get started with Regression.

Regression

Linear Regression

What is Linear Regression?

Linear regression is a basic and commonly used type of predictive analysis. The overall idea of regression is to examine two things:

• Does a set of predictor variables do a good job in predicting an outcome (dependent) variable?
• Which variables in particular are significant predictors of the outcome variable, and in what way do they impact the outcome variable?
  These regression estimates are used to explain the relationship between one dependent variable and one or more independent variables.

The simplest form of the regression equation with one dependent and one independent variable is defined by the formula ** y = c + b*x**, where

• y = estimated dependent variable score,
• c = constant (y intercept),
• b = regression coefficient (slope), and
• x = score on the independent variable.

For example, in the task of predicting the house prices, the different attributes of the house such as no of bedrooms, carpet area, proximity to hospital, etc. become the independent variables (X: x1, x2, x3,…) while the price estimate of the house becomes the dependent variable(Y).

Three major uses for regression analysis:

• First, the regression might be used to identify the strength of the effect that the independent variable(s) have on a dependent variable. Typical questions are what is the strength of relationship between dose and effect, sales and marketing spending, or age and income.
• Second, it can be used to forecast effects or impact of changes. That is, the regression analysis helps us to understand how much the dependent variable changes with a change in one or more independent variables. A typical question is, “how much additional sales income do I get for each additional $1000 spent on marketing?”
• Third, regression analysis predicts trends and future values. The regression analysis can be used to get point estimates. A typical question is, “what will the price of gold be in 6 months?”

Follow these links for more detailed explanation:

• What is Linear Regression
• Gradient Descent

• Linear Regression from scratch

• Linear Regression using Sklearn

Linear Regression From scratch

import numpy as np
from statistics import mean
import matplotlib.pyplot as plt
from matplotlib import style
import random

style.use('fivethirtyeight')

xs = np.array([1,2,3,4,5,6])
ys = np.array([5,4,6,5,6,7])

#xs = np.array([1,2,3,4,5,6])
#ys = np.array([1,2,3,4,5,6])

def best_fit_slope_and_intercept(xs,ys):
    m = ( ((mean(xs)*mean(ys))-mean(xs*ys))/
        ((mean(xs)**2) - mean(xs*xs)) )
    b = np.mean(ys) - m*np.mean(xs)
    return m,b

def sq_error(y_orig, y_line):
    return sum((y_line - y_orig)**2)

#R-square error
def coeff_of_determination(y_orig, y_line):
    y_mean_line = [mean(y_orig) for y in y_orig]
    sq_err_reg = sq_error(y_orig, y_line)
    sq_err_mean = sq_error(y_orig, y_mean_line)
    return 1 - (sq_err_reg/sq_err_mean)

def linearreg_predictior(xs,ys,pred_x):
    m,b = best_fit_slope_and_intercept(xs,ys)
    reg_line = [(m*x)+b for x in xs]
    pred_y = (m*pred_x) + b
    plt.scatter(xs,ys)
    plt.plot(xs, reg_line)
    plt.scatter(pred_x, pred_y)
    plt.show()
    
    r_sq = coeff_of_determination(ys,reg_line)
    print(r_sq)
    return None

linearreg_predictior(xs,ys,4.5)

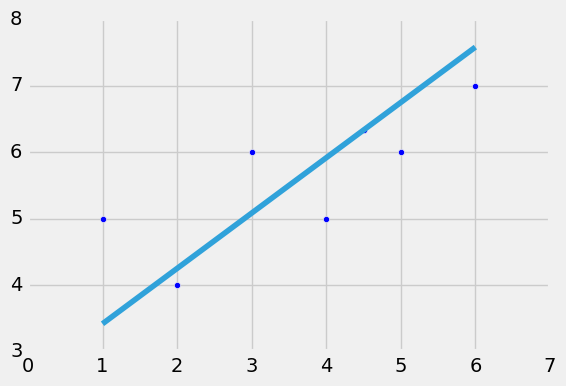
0.263888888889

The points on the graph are the input data points and the line is the best-fit line for the given input data.

R-Square: It determines how much of the total variation in Y (dependent variable) is explained by the variation in X (independent variable).

scikit learn code

Steps To Be followed When Applying an Algorithm using Sklearn (ML Pipeline):

• Split the dataset into training and testing dataset. The testing dataset is generally smaller than training one as it will help in training the model better.
• Select any algorithm based on the problem (classification or regression). Not every algorithm is suitable for all the problems.
• Then pass the training dataset to the algorithm to train it. We use the .fit() method
• Then pass the testing data to the trained algorithm to predict the outcome. We use the .predict() method.
• We then check the accuracy by passing the predicted outcome and the actual output to the model.

# importing basic libraries

import numpy as np
import pandas as pd
from pandas import Series, DataFrame
from sklearn.model_selection import train_test_split

#importing dataset

train = pd.read_csv('Train_BigMartSales.csv',encoding = "ISO-8859-1")
test = pd.read_csv('Test_BigMartSales.csv',encoding = "ISO-8859-1")

# importing linear regressionfrom sklearn
from sklearn.linear_model import LinearRegression
test.head()

	Item_Identifier	Item_Weight	Item_Fat_Content	Item_Visibility	Item_Type	Item_MRP	Outlet_Identifier	Outlet_Establishment_Year	Outlet_Size	Outlet_Location_Type	Outlet_Type
0	FDW58	20.750	Low Fat	0.007565	Snack Foods	107.8622	OUT049	1999	Medium	Tier 1	Supermarket Type1
1	FDW14	8.300	reg	0.038428	Dairy	87.3198	OUT017	2007	NaN	Tier 2	Supermarket Type1
2	NCN55	14.600	Low Fat	0.099575	Others	241.7538	OUT010	1998	NaN	Tier 3	Grocery Store
3	FDQ58	7.315	Low Fat	0.015388	Snack Foods	155.0340	OUT017	2007	NaN	Tier 2	Supermarket Type1
4	FDY38	NaN	Regular	0.118599	Dairy	234.2300	OUT027	1985	Medium	Tier 3	Supermarket Type3

#Now follow the steps according to the ML Pipeline
#splitting into training and cv for cross validation

X = train.loc[:,['Outlet_Establishment_Year','Item_MRP']]
x_train, x_cv, y_train, y_cv = train_test_split(X,train.Item_Outlet_Sales)

#training the model
clf = LinearRegression()
clf.fit(x_train,y_train)

#predicting on cv

pred = clf.predict(x_cv)

#calculating mse

mse = np.mean((pred - y_cv)**2)

r_sq = clf.score(x_cv,y_cv)

print("R-square ",r_sq)


## calculating coefficients

coeff = DataFrame(x_train.columns)

coeff['Coefficient Estimate'] = Series(clf.coef_)
print(coeff)

R-square  0.342111766614
                           0  Coefficient Estimate
0  Outlet_Establishment_Year            -13.386884
1                   Item_MRP             15.426249

Follow these link for detailed explanation

• Linear Regression

• Lasso and Ridge Regression

• Types of Regression Techniques

We hope this post was helpful. Feel free to comment in case of doubts and do let us know your feedback. Stay tuned for more!