Feature Scaling & Mean Normalization
Since the range of values of raw data varies widely, in some machine learning algorithms, objective functions will not work properly without normalization. For example, the majority of classifiers calculate the distance between two points by the Euclidean distance. If one of the features has a broad range of values, the distance will be governed by this particular feature. Therefore, the range of all features should be normalized so that each feature contributes approximately proportionately to the final distance.
Feature scaling is a method used to standardize the range of independent variables or features of data.
The simplest method is rescaling the range of features to scale the range in [0, 1] or [−1, 1]. Selecting the target range depends on the nature of the data. The general formula is given as:
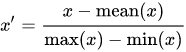
where x is an original value, x’ is the normalized value. For example, suppose that we have the students’ weight data, and the students’ weights span [160 pounds, 200 pounds]. To rescale this data, we first subtract 160 from each student’s weight and divide the result by 40 (the difference between the maximum and minimum weights).
Mean normalization is used to make features have approximate zero mean.
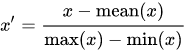
Another reason why feature scaling and mean normalization are applied is that gradient descent converges much faster with feature scaling than without it.
Bias & Variance - Problem of underfitting and overfitting
In supervised machine learning an algorithm learns a model from training data. The goal of any supervised machine learning algorithm is to best estimate the mapping function (f) for the output variable (Y) given the input data (X). The mapping function is often called the target function because it is the function that a given supervised machine learning algorithm aims to approximate.
The prediction error for any machine learning algorithm can be broken down into three parts:
- Bias Error: Bias are the simplifying assumptions made by a model to make the target function easier to learn.
- Variance Error: Variance is the amount that the estimate of the target function will change if different training data was used.
- Irreducible Error: It cannot be reduced regardless of what algorithm is used. It is the error introduced from the chosen framing of the problem and may be caused by factors like unknown variables that influence the mapping of the input variables to the output variable.
Underfitting / High Bias
A statistical model or a machine learning algorithm is said to have underfitting when it cannot capture the underlying trend of the data. Its occurrence simply means that our model or the algorithm does not fit the data well enough. It usually happens when we have less data to build an accurate model and also when we try to build a linear model with a non-linear data. Underfitting can be avoided by using more data and also reducing the features by feature selection.
Overfitting/ High Variance
A statistical model is said to be overfitted, when we train it with a lot of data. When a model gets trained with so much of data, it starts learning from the noise and inaccurate data entries in our data set. Then the model does not categorize the data correctly, because of too much of details and noise. The causes of overfitting are the non-parametric and non-linear methods because these types of machine learning algorithms have more freedom in building the model based on the dataset and therefore they can really build unrealistic models.
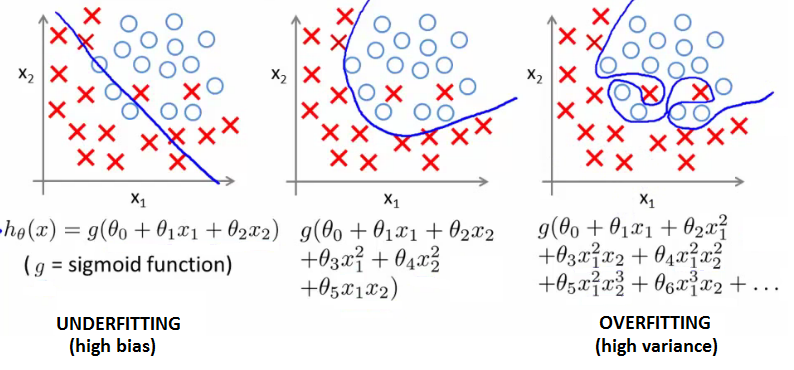
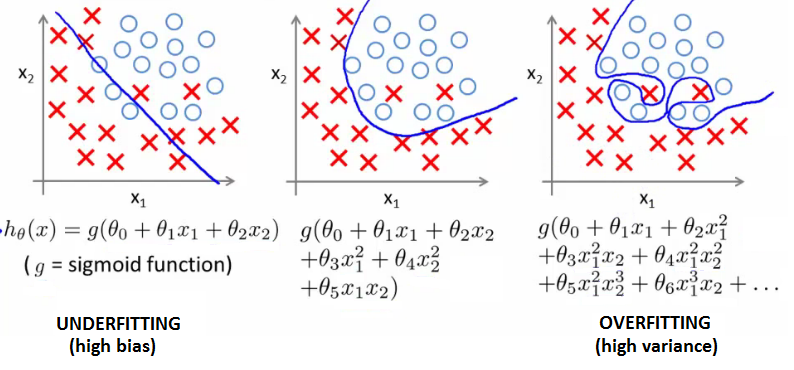
How to avoid underfitting:
- Adding more number of features
- Adding polynomial features
How to avoid overfitting:
- Get more data
- Reduce number of features by feature selection
- Regularization
Regularization
- To prevent overfitting, You must minimize the values of the parameters theta. To do so, YOu introduce another parameter lambda into the fray. Regularization is a very effective mechanism as it also provides a simpler hypothesis and smoother curves.
- The regularization parameter lambda will control the trade-off between keeping the parameters small aand fitting the data well. If you set the lambda value to be very large, You’ll end up penalizing all the parameters such that all the values of theta will be close to 0 which results in underfitting. If the value of lambda is very small, It won’t be much effective.
- To implement regularization, you add another term to the cost function as shown in the image.
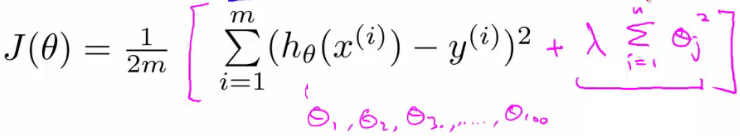
- This form of regularization is also called as L1-regularization. L1-regularization is one of the many techniques for regularization.
The different regularization techniques are as follows:
1. L2-regularization / Weight-Decay
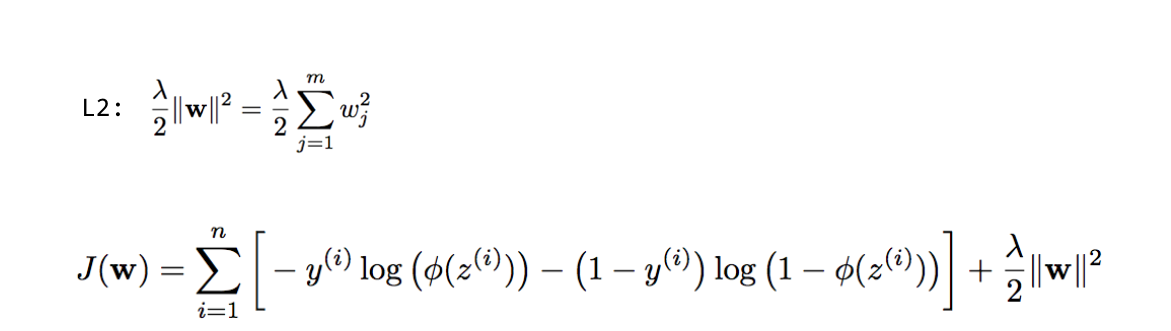2. Dropout regularization
In this method, At each training stage, individual nodes are either “dropped out” of the net with probability 1-p or kept with probability p, so that a reduced network is left; incoming and outgoing edges to a dropped-out node are also removed. Only the reduced network is trained on the data in that stage. The removed nodes are then reinserted into the network with their original weights. The following image depicts how dropout works.
By avoiding training all nodes on all training data, dropout decreases overfitting. The method also significantly improves training speed.
3. Data Augmentation - Sometimes, collection of training data is often expensive and laborious. Data augmentation overcomes this issue by artificially inflating the training set with label preserving transformations.
- For example, if you have an image dataset, you could add more examples to the dataset by changing the orientation of an existing image in the dataset and add it as an independent image in the dataset. Similarly, you can add random distortions and rotations as independent units in the dataset. 4. Early stopping
- Gradient Descent is used to update the learner so as to make it better fit the training data with each iteration.
- Up to a point, this improves the learner’s performance on data outside of the training set.
- Past that point, however, improving the learner’s fit to the training data comes at the expense of increased generalization error.
- Early stopping rules provide guidance as to how many iterations can be run before the learner begins to over-fit.
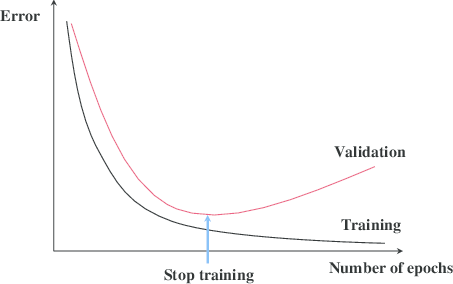
Learning curves
- Learning curve is a plot between the training set size and the error obtained from the cost function.
- Learning curves can be used to determine whether the model has underfit or overfit.
- Once you know if there is high bias or high variance, you can either add more features or more examples/data as required.
- An in-depth explanation of Learning curves is given here
Dataset split
- Usually, the entire dataset is split into a training dataset, a cross-validation dataset and a test dataset.
- The training dataset should contain the bulk of the examples, with a few examples in the CV set and test set respectively.
- Conventionally, the dataset split is 60/20/20 percentage wise. But, this percentage split is subjective. For example, if there are a million examples in the dataset, the CV set and test set will contain 2 million examples each which is not required. So, the split should be done considering the size of the dataset.
- When there is a big difference between the error in the training set(training error)and the error in the test set (test error), It is said to have a high variance.
- When the training error itself is high, the model is said to have underfit or is said to have high bias.
- More insights here
Initialization methods
There are two methods of initialization: Zero Initialization and Random Initialization.
- Zero Initialization : The parameters are initialized to zero.
- Random Initialization : The parameters are initialized with random values.
- There is a problem with Zero initialization called as Symmetry breaking. If all of the weights are the same (i.e 0), they will all have the same error and the model will not learn anything - there is no source of asymmetry between the neurons.
- What we could do, instead, is to keep the weights very close to zero but make them different by initializing them to small, non-zero numbers.It has the same advantage of all-zero initialization in that it is close to the ‘best guess’ expectation value but the symmetry has also been broken enough for the algorithm to work.
- Hence, it is generally advised to go with random initialization of parameters / weights.
Performance Measures
- We already have seen Accuracy as a performance measure. There are three more performance measures which are as follows:
- Precision - It is the ratio of correctly predicted positive observations to the total predicted positive observations.
- Recall - Ratio of correctly predicted positive observations to all the correctly predicted observations in the class.
- F-Score - Harmonic mean / Weighted average of Precision and Recall.
- Check this blog for a better understanding of these measures
Principal Component Analysis (PCA)
- PCA is one of the most commonly used algorithms for dimensionality reduction.
- PCA speeds up supervised learning; it is also used to prevent overfitting which is a bad use of the algorithm.
- Problem Formulation - Trying to find a dimensional surface such that the projectional error is minimized.
- One should make sure that the features are scaled and mean normalized before applying PCA.
- More insights on PCA here
Ensembling Models
Not every Machine Learning algorithm is suitable for all types of problems. SVM may work well with one dataset but it may lack in some other problem. Now let’s consider a problem in classification, where we need to classify the dataset into 2 classes say, 0 and 1. Consider the following situation:
Let’s use 2 algorithms viz SVM and Logistic Regression, and we build 2 different models and use it for classification. Now when we apply our model on the test data, we see that SVM is able to correctly classify the data belonging to Class 0 (i.e data belonging to class 0 is correctly classified as Class 0), whereas it doesn’t work well for the data belonging to Class 1 (i.e data belonging to class 1 is wrongly classified as Class 0 ). Similarly Logistic Regression works very well for Class 1 data but not for Class 0 data. Now if we combine both of these models (SVM and Logistic Regression) and create a hybrid model, then don’t you think the hybrid model will work well with data belonging to both the classes?? Such a hybrid model is known as an Ensemble Model.
Ensembling is a good way to increase or improve the accuracy or performance of a model. In simple words, it is the combination of various simple models to create a single powerful model. But there is no guarantee that Ensembling will improve the accuracy of a model. However it does a good stable model as compared to simple models.
Ensembling can be done in ways like:
-
Voting Classifier
-
Bagging
-
Boosting.
Voting Classifier
It is the simplest way of combining predictions from many different simple machine learning models. It gives an average prediction result based on the prediction of all the submodels. The submodels or the basemodels are all of diiferent types.
import pandas as pd
import numpy as np
from sklearn import svm #support vector Machine
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split #training and testing data split
from sklearn import metrics #accuracy measure
from sklearn.model_selection import cross_val_score #score evaluation
from sklearn.model_selection import cross_val_predict #prediction
diab=pd.read_csv('diabetes.csv')
diab.head(3)
| Pregnancies | Glucose | BloodPressure | SkinThickness | Insulin | BMI | DiabetesPedigreeFunction | Age | Outcome | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148 | 72 | 35 | 0 | 33.6 | 0.627 | 50 | 1 |
| 1 | 1 | 85 | 66 | 29 | 0 | 26.6 | 0.351 | 31 | 0 |
| 2 | 8 | 183 | 64 | 0 | 0 | 23.3 | 0.672 | 32 | 1 |
outcome=diab['Outcome']
data=diab[diab.columns[:8]]
train,test=train_test_split(diab,test_size=0.25,random_state=0,stratify=diab['Outcome'])# stratify the outcome
train_X=train[train.columns[:8]]
test_X=test[test.columns[:8]]
train_Y=train['Outcome']
test_Y=test['Outcome']
Lets create 2 simple models and check the accuracy
SVM
SVM=svm.SVC(probability=True)
SVM.fit(train_X,train_Y)
prediction=SVM.predict(test_X)
print('Accuracy for SVM kernel is',metrics.accuracy_score(prediction,test_Y))
Accuracy for SVM kernel is 0.651041666667
Logistic Regression
LR=LogisticRegression()
LR.fit(train_X,train_Y)
prediction=LR.predict(test_X)
print('The accuracy of the Logistic Regression is',metrics.accuracy_score(prediction,test_Y))
The accuracy of the Logistic Regression is 0.776041666667
Voting Classifier
from sklearn.ensemble import VotingClassifier #for Voting Classifier
ensemble_lin_rbf=VotingClassifier(estimators=[('svm', SVM), ('LR', LR)],
voting='soft',weights=[1,2]).fit(train_X,train_Y)
print('The accuracy for Ensembled Model is:',ensemble_lin_rbf.score(test_X,test_Y))
The accuracy for Ensembled Model is: 0.78125
You can see clearly that the accuracy for the Voting Classifier is higher as compared to the simple models.
Bagging
Bagging is a general ensemble method. It works by applying similar classifiers on small partitions of the dataset and then taking the average of all the predictions. Due to the averaging,there is reduction in variance. Unlike Voting Classifier, Bagging makes use of similar classifiers.
Bagged KNN
Bagging works best with models with high variance. An example for this can be Decision Tree or Random Forests. We can use KNN with small value of n_neighbours, as small value of n_neighbours.
from sklearn.ensemble import BaggingClassifier
from sklearn.neighbors import KNeighborsClassifier
model=BaggingClassifier(base_estimator=KNeighborsClassifier(n_neighbors=3),random_state=0,n_estimators=700)
model.fit(train_X,train_Y)
prediction=model.predict(test_X)
print('The accuracy for bagged KNN is:',metrics.accuracy_score(prediction,test_Y))
The accuracy for bagged KNN is: 0.744791666667
Boosting
Boosting is an ensembling technique which uses sequential learning of classifiers. It is a step by step enhancement of a weak model.Boosting works as follows:
A model is first trained on the complete dataset. Now the model will get some instances right while some wrong. Now in the next iteration, the learner will focus more on the wrongly predicted instances or give more weight to it. Thus it will try to predict the wrong instance correctly. Now this iterative process continous, and new classifers are added to the model until the limit is reached on the accuracy.
AdaBoost(Adaptive Boosting)
The weak learner or estimator in this case is a Decsion Tree. But we can change the dafault base_estimator to any algorithm of our choice.
Now for AdaBoost, we will directly run the Cross Validation Test, i.e we will run the algorithm on the entire dataset and check the mean accuracy for the ensemble model.
from sklearn.ensemble import AdaBoostClassifier
X=diab[diab.columns[:7]]
Y=diab['Outcome']
ada=AdaBoostClassifier(n_estimators=300,random_state=0,learning_rate=0.1)
result=cross_val_score(ada,X,Y,cv=10,scoring='accuracy')
print('The cross validated score for AdaBoost is:',result.mean())
The cross validated score for AdaBoost is: 0.763004101162
Looking at the above results, you might be thinking that Voting Classifier might always give the highest accuracy. But as we have discussed earlier, not every algorithm is for every problem. Many other factors like the hyperparameters, class imbalance, etc affect the efficiency of the model. In the above cases, if we make changes in some hyperparameters, it might be possible that AdaBoost or Bagging would give a better results. Thus we must always try out every method available.
Further Readings:
Ensembling Theory and Implementation
We hope this post was helpful. Feel free to comment in case of doubts and do let us know your feedback. Stay tuned for more!